NÚMEROS DECIMALES
En el mes de Febrero, hemos visto en clase los números decimales; estos se utilizan para representar números más pequeños que la unidad y es la expresión de un número no entero que tiene una parte decimal; por tanto, tiene una parte entera y una parte decimal que va separada por una coma (3,78).
Los números decimales se escriben a la derecha de las unidades los cuales están separados por una coma, estas son las centenas, decenas, unidades , décimas, centésimas y milésimas.
En la clasificación de los decimales podemos encontrar:
- Decimales exactos: 2,4 -> los decimales son limitados
- Decimales periódicos: 2, 444... -> los decimales son infinitos y siempre se repite.
- Decimales periódicos mixtos: 2,4333... --> los decimales son infinitos pero delante hay decimales fuera del patrón
SUMA Y RESTA DE DECIMALES
Para sumar y restar números decimales se deberán colocar en vertical y la coma debemos hacer que coincidan todas en la misma columna independientemente de si hay más cifras en un número entero, así, coincidiendo las unidaes, decenas, centenas, etc... y los decimales con los decimales.
A continuación se realizará la suma o la resta correspondiente, colocanco en el resultado final la coma en la columna correspondiente.
Ejemplos:
MULTIPLICACIÓN DECIMALES
Cuando vamos a realizar una multiplicacion de dos números decimales o un número decimal con uno entero, la multiplicación se realiza sin tener en cuanta la coma; a continuación, una vez resuelta la operación, se suman todos los decimales que hay en los números que se han multiplicado entre sí, y contando desde el final del resultado que hemos obtenido a la izquierda se mueve la coma tantos lugares como decimales hayamos sumado en los números que se han multiplicado.
- Multiplicación por el número 10, 100, 1000, 10000, etc
En este tipo de multiplicación con números decimales sólo tendremos que mover la coma a la derecha como tantos "0" haya; ya que un número multiplicado por "1" da como resultado el mismo número sólo habrá que tener en cuenta los "0" que haya en las decenas, centenas, unidades de millar, etc...
Ejemplos:
- 5,98 x 10 = 59,8
- 87,24 x 100 = 8724
- 3,0868 x 1000 = 3086,8
DIVISIÓN DE DECIMALES
En la división de los decimales podemos encontrar varios casos distintos dependiendo de cómo estén colocados en el dividor, dividendo o en los dos. En los ejercicios que vamos a encontrar, el dividendo es el número decimal. Al realizar la división no se tiene en cuanta la la coma pero al tener la primera cifra decimal se pone en el resultado y se sigue dividiendo de igual forma. Otro caso que podemos encontrar es cuando el número decimal se encuentra en el divisor, aquí deberemos correr la coma hasta el final del número y miemtras añadimos un cero al dividendo por laca lugar que movemos la coma. A continuación se divide de manera normal hasta obtener un resulado. La división 65:0,15, quedaría 6500:15.
Ejemplos:
- División por el número 10, 100, 1000, 10000, etc
El siguiente caso vamos a encontar un número decimal que va a ser dividido por una cifra múltiplo de diez. Para realizar la operación debemos mover la coma hacia el lado izquierdo dependiendo los ceros que tenga el número múltiplo de diez. Si supera el número de espacios que tenemos que mover se colocarán ceros a la izquierda, una vez colocados todos los ceros si se diese este caso, colocaríamos una coma y un cero delante de esta para obtener el resultado final.
Ejemplos:
- 5,98 : 10 =0,598
- 8,724 : 100 = 0,08724
- 3086,8 : 1000 = 3,0868
EJERCICIOS PARA PRACTICAR
1. Suma de decimales
- 342.528 + 6 726.34 + 5.3026 + 0.37=
- 2,42 + 3,7 + 4,128 =
- 40,036 + 385 =
- 32,045 + 123,7 =
- 0,19 + 3,81 + 22,2 =
2. Resta de decimales
- 372,528 - 69,68452 =
- 9,1 - 3,82 =
- 123,766 - 35,4 =
- 157,83 - 48,092 =
- 120,45 - 10,3 =
3. Multiplicación de decimales
- 5,2 x 10 =
- 5,2 x 100 =
- 5,2 x 1000 =
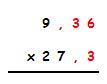
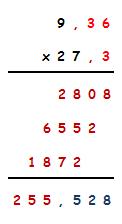
- 4,31 x 2,6 =
- 1,42 x 1,3 =
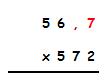
- 56,7 x 572 =
- 39,8 x 12 =
- 2,35 x 0,21=
4. División de decimales
- 24,2 : 10 =
- 24,2 : 100 =
- 24,2 : 1000 =
- 7,36 : 2 =
- 4,326 : 3 =
- 32,156 : 4 =
- 267,05 : 5 =
- 39,120 : 6 =
RESOLUCIÓN DE EJERCICIOS
1. Suma de decimales
- 7,074,5406
- 10,248
- 425,036
- 155,745
- 26,20
2. Resta de decimales
- 302,84348
- 5,28
- 88,366
- 109,738
- 110,15
3. Multiplicación de decimales
- 52
- 520
- 5200
- 11,206
- 1, 846
- 32432,4
- 477,6
- 0,4935
4. División de decimales
- 2,42
- 0,242
- 0,0242
- 3,68
- 1,442
- 8,039
- 53,41
- 6,52



















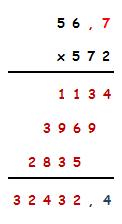



















 600 alumnos
600 alumnos