Los niveles de Van Hiele (Pierre Van Hiele y Dina Van Diele- Geldof) - 1957.
Publicaron un libro "Structure and Insight: A theory of mathematics education" donde se desarrolla la teoría (estudio centrado en la Geometría, cinco niveles jerárquicos aplicados en tareas y situaciones adaptadas a estudiantes).
Dicha teoría sirve para que los estudiantes puedan comprender y orientarse en el desarrollo del pensamiento geométrico.
Esta teoría abarcó numerosas investigaciones y experimentaciones, las cuáles llevaron a introducir diversos matices en el estudio. A pesar de ello, se sigue a día de hoy utilizando la teoría de "Los niveles de Van Hiele" pues resultan útiles para organizar el currículo de Geometría.
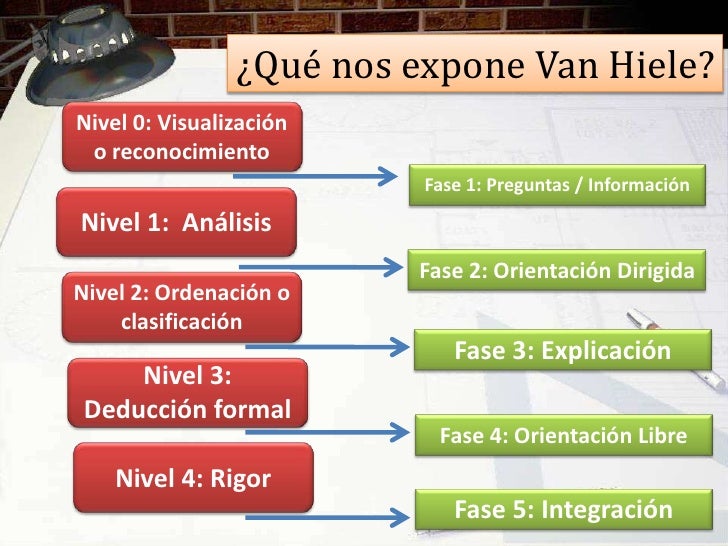
Los 5 niveles de Van Hiele: Desarrollo del razonamiento geométrico.
(Cada nivel describe los procesos de pensamiento aplicados a tareas y situaciones geométricas).
→ La mayoría de estudiantes (no universitarios) alcanzan hasta los 3 primeros niveles. Educación primaria: (N-0, N-1, N-2)
- Nivel 0: Visualización. (Los objetos de pensamiento son formas individuales, formas singulares. Los alumnos son capaces de hacer mediciones. Su tarea, consiste en reconocer las figuras y nombrar las características visuales globales. Se conciben los objetos por su forma, su apariencia).
*Actividades de clasificación, identificación, descripción de formas variadas. Uso de objetos físicos que sean manipulables para los niños (formas diferentes y variadas).
- Nivel 1: Análisis. (Los objetos de pensamiento son clases de formas, las características irrelevantes pasan a un segundo plano. Ya que los alumnos deben considerar todas las formas incluidas en una clase de forma particular). Por ejemplo: En vez de hablar sobre un rectángulo singular, hablar de toda clase de rectángulos. Pensar en las propiedades que conforman dicha figura.
*Actividades con objetos de un modelo concreto en el que se centren en sus propiedades. También es posible usar modelos de exploración (diversas propiedades).
- Nivel 2: Deducción informal. (Los objetos de pensamiento, son las propiedades de las formas. Los alumnos, deben pensar en las propiedades (sin restricciones de un objeto o figura en particular). Llegando a desarrollar relaciones entre estas propiedades).
*Actividades en las que centren su atención en la definición de propiedades. Uso lenguaje apropiado (naturaleza deductiva e informal). Investigar la validez de ciertas relaciones entre propiedades.
- Nivel 3: Deducción. (Los objetos de pensamiento, son relaciones de las propiedades de los objetos geométricos. Los alumnos elaboran deducciones dentro de un sistema, examinan más allá de las propiedades; deben analizar argumentos informales, sistemas axiomáticos, definir teoremas, etc.)Nivel 3, dirigido a alumnos de educación superior Bachillerato (geometría).
Nivel 4: Rigor. (La jerarquía de pensamiento geométrico, el objeto de pensamiento se centra en el propio sistema axiomático. Sin recurrir a sistemas deductivos dentro de un sistema). Nivel 4, dirigido a estudiantes universitarios especializados en geometría (rama de matemáticas).