Durante la primera quincena del mes de Mayo hablaremos del Teorema de Pitágoras y la formula de este para el Triángulo Rectángulo.
INTRODUCCIÓN DEL TEOREMA DE PITÁGORAS
El Teorema de Pitágoras es una teoría que inventó Pitágoras de Samohace muchos años y hasta día de hoy sigue siendo una teoría muy utilizada por las personas para estudiar en la escuela o también para resolver problemas en el día a día. Pitágoras señala que en un triángulo rectángulo, podemos saber lo que miden todos sin saber la longitud de uno de ellos. ¿Cómo podemos hacer esto? Gracias a la fórmula del Teorema de Pitágoras.
FORMULA DEL TRIÁNGULO RECTÁNGULO
Pero antes de llegar hasta aquí es importante saber el nombre de los lados de un triángulo rectángulo. Por una parte, tenemos los lados pequeños que se llaman catetos y por otra parte, el lado más grande que se llama hipotenusa. La hipotenusa en el Teorema de Pitágoras, con su tamaño, forma un ángulo de 90º que es el ángulo recto de nuestro triángulo, y los catetos son aquellos que están en el lado opuesto de este ángulo recto
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
a
2=b2+c2 triángulo rectángulo
Ejemplos del Teorema de Pitágoras
A continuación expondremos ejemplos del Teorema de Pitágoras para niños para entender un poco mejor la explicación del teorema de Pitágoras para niños y para ello, explicaremos qué es la fórmula del Teorema de Pitágoras. Así pues, según la fórmula del Teorema de Pitágoras, si sumamos los catetos y el resultado lo multiplicamos por el mismo número, es decir lo elevamos a 2, o al cuadrado, el número resultante será igual a la hipotenusa elevada al cuadrado. Por lo tanto quedaría así:
(H2 = X² + Y²) o (H=√X²+ Y²)
Ahora bien, si, por ejemplo, los catetos tienen una longitud de 5cm el resultado de la fórmula del Teorema de Pitágoras sería 7,1 cm puesto que la ecuación quedaría así:
H= √5² + 5²
EJERCICIOS RESULTOS
A cotinuación ponemos unos ejercicios para que puedan practicar en casa
Problema 1
Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.
Los lados son
Aplicando el teorema de Pitágoras,
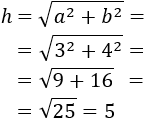
Por tanto, la hipotenusa mide 5cm.
Problema 2
Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1cm, ¿cuánto mide el otro lado?
Llamamos a los lados a y b y a la hipotenusa h. Sabemos que
Por Pitágoras, sabemos que
Sustituyendo los valores conocidos tenemos que
 Ahora despejamos b en la ecuación
Ahora despejamos b en la ecuación
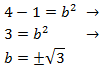 Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.
Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.
Por tanto, el cateto mide
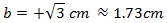 Podemos dejar la raíz cuadrada o aproximarla
Podemos dejar la raíz cuadrada o aproximarla
.
 Calcular cuánto mide la hipotenusa.
Calcular cuánto mide la hipotenusa.
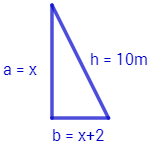 ¿Cuánto miden los catetos?
¿Cuánto miden los catetos?
Por Pitágoras, sabemos que
Sustituyendo los valores conocidos tenemos que

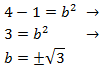
Por tanto, el cateto mide
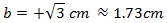
.
Problema 1
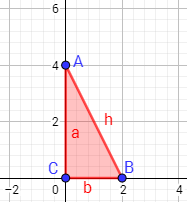
En el siguiente triángulo, ¿cuál de los lados es la hipotenusa y cuál es el ángulo recto?
Los catetos son los lados y . La hipotenusa es el lado . El ángulo recto es el ángulo que forman ambos catetos.
Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden y , con lo que
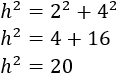 Finalmente, hacemos la raíz cuadrada:
Finalmente, hacemos la raíz cuadrada:
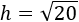 Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
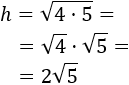 Si aproximamos, .
Si aproximamos, .
Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden y , con lo que
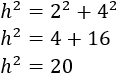
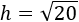
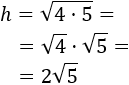
Problema 4
La hipotenusa de un triángulo rectángulo mide 10 metros y sus catetos miden y :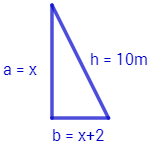
Solución
Por Pitágoras, , con lo que
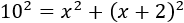 No olvidemos la fórmula del cuadrado de un binomio:
No olvidemos la fórmula del cuadrado de un binomio:
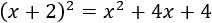 Sustituyendo,
Sustituyendo,
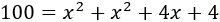 Simplificamos la ecuación:
Simplificamos la ecuación:
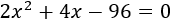 Resolvemos la ecuación de segundo grado:
Resolvemos la ecuación de segundo grado:
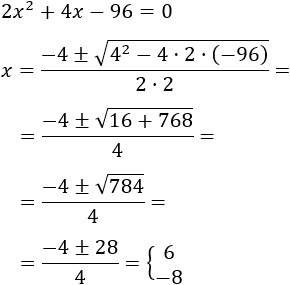 Como representa una longitud, la solución debe ser positiva: . Los catetos miden 6 y 8 metros.
Como representa una longitud, la solución debe ser positiva: . Los catetos miden 6 y 8 metros.
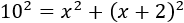
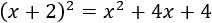
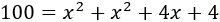
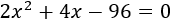
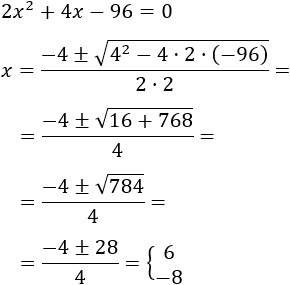


No hay comentarios:
Publicar un comentario