Tema 3: Geometría. "Figuras geométricas: Poliedros, Cilindro y Cono"

Dando continuación al bloque de "Geometría" (una vez se ha desarrollado el apartado de figuras geométricas 2D). 

*(CLASE) Como breve introducción, se dará un pequeño repaso que refuerce los conceptos y contenidos relacionados (ya aprendido cursos anteriores). Resulta vital y necesario que los alumnos empiecen este apartado con una base (refuerzo) de conocimientos y aplicación, sobre Geometría. En ocasiones, dichos conceptos no se aprenden correctamente. Por lo que en este caso, los cuerpos geométricos suelen dar cabida a confusiones (por la similitud de ciertos cuerpos geométricos, entre sí). Para ello, estableceremos relaciones entre las distintas figuras, explicando las características básicas de cada figura. (Soporte del medio, "Geogebra" en el que los alumnos pueden visualizar y representar de forma sencilla: las figuras geométricas (3D) para facilitar su comprensión).

Finalmente dicho refuerzo introductorio les va a resultar útil, especialmente a la hora de comprender y trabajar con dicho apartado.

Geometría (3D) referida a las siguientes figuras geométricas: (poliedro, cilindro y cono). 

Denominadas "figuras en el espacio", por estar representadas en un plano tridimensional (3D): (son tres conjuntos disjuntos: propio plano y dos semi-espacios). 

Este grupo de figuras tridimensionales se clasifica, a su vez en 2 sub-grupos: 

• Los Poliedros: Cuerpos geométricos limitados por polígonos (prismas, pirámides o polígonos regulares), divididos según su carácter:

               -Cóncavo: Alguno de sus ángulos es cóncavo, debido a que alguna cara del                                           poliedro, no puede apoyarse en un plano.

             -Convexo: Todos sus ángulos son convexos, debido a que todas sus caras se                                         pueden apoyar sobre un plano. 

   

           * Los poliedros convexos, pueden ser: 

              - Irregulares: Prisma y pirámide.

              - Regulares: formados por polígonos regulares idénticos. 

        Se cumple con la relación "Teoría de Euler": (C+V = A+2). Todo poliedro                          convexo,  cumple que el número de caras (C) más el número de vértices (V) es                 igual al número de aristas (A) más 2. 

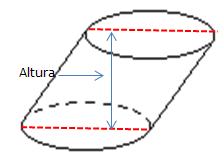
• Los Sólidos de revolución: "Cuerpos Redondos". Son cuerpos geométricos que no están delimitados por polígonos, sino por alguna superficie curva, como el cilindro, el cono y la esfera.

            - Esfera se genera al girar una semicircunferencia alrededor de un eje.

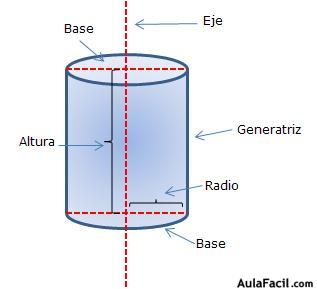
           - Cilindro surge al girar un rectángulo alrededor de uno de sus lados.

          

Cilindro Oblicuo: Resulta de cortar oblicuamente un cilindro recto con dos planos paralelos. Las bases se denominan "Elipses", su altura es la distancia entre los planos que contienen las bases.

• Eje: lado sobre el que el rectángulo gira para generar el cilindro.
• Altura: longitud del eje del cilindro.
• Generatriz: lado que genera la superficie lateral del cilindro o es la longitud del lado opuesto al eje.
• Base: son dos circulos paralelos e iguales que se generan al girar los lados perpendiculares al eje.
• Radio: longitud de los lados perpendiculares al eje o el radio de la base.

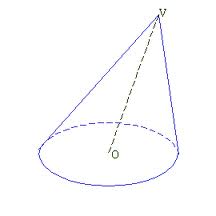
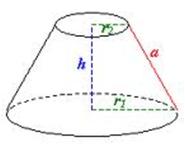
            - Cono es un sólido que resulta al girar un triángulo recto alrededor de uno de                      sus catetos (eje). Tiene una sola base en forma de círculo y una cara lateral                      curva que finaliza en un punto llamado vértice o cúspide. 

• Eje: cateto sobre el que gira el triángulo para generar el cono.
• Altura: longitud del eje.
• Generatriz: longitud de la hipotenusa del triángulo.
• Base: círculo general al girar el cateto perpendicular al eje.
• Radio: radio de la base o longitud del cateto perpendicular al eje.

  

    * Cono Inclinado: Se obtiene cortando un cono de forma oblicua con un plano. La base de un                                                         cono inclinado no es circular sino que tiene forma de elipse.

    * Tronco de cono: Figura que se obtiene al cortar un cono con un plano horizontal.

PRÁCTICA EN CASA: 

1. Calcula, ¿cuántas aristas (A) tiene un prisma cuadrangular? 

* SOLUCIÓN: 

   Supongamos tenemos un prisma cuadrangular. Éste tiene seis caras (C=6) que                 son las dos bases y los cuatro paralelogramos de los laterales. También es                       conocido el número de vértices que tiene (V=8).  

   -Resolvemos poniendo en práctica la relación de "Tª Euler":

Y se obtiene que tiene doce aristas, A=12.

2. En cada uno de los siguientes poliedros indica el numero de caras, aristas y             vertices.

- Tetraedro             - Hexaedro regular (cubo)

- Octaedro                   
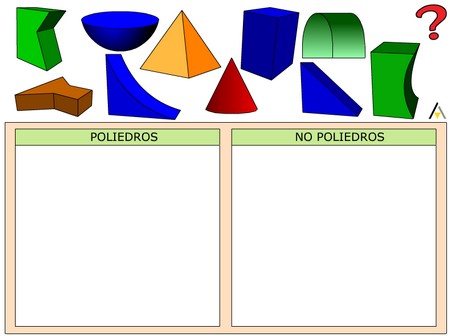
                                                                                                                          3. ¿Cúales son poliedros?, ¿Cuáles no?