Tema 6: "Primer enunciado del teorema de Tales"

Tras profundizar en el "Teorema de Tales (Thales)" una de las teorías más conocidas en Geometría → (necesario saber cuál es la razón o relación entre dos segmentos)

Thales de Mileto desarrolla 2 enunciados geométricos, dentro del propio teorema: "Teorema fundamental de la Semejanza entre triángulos" o conocido como "Teorema particular de Tales"

Los enunciados de Tales recogen aspectos importantes sobre la Geometría básica. En este caso, vamos a desarrollar →

1. Primer enunciado: "Los segmentos (dos rectas) son proporcionales". 

Al cortar los lados de un ángulo cualquiera por dos rectas paralelas, los segmentos de una de las rectas es proporcional a los segmentos correspondientes de la otra recta. "Proporcionalidad geométrica"

Representación:

Si dos rectas (r y r´) se cortan por varias rectas paralelas (AA’, BB’, CC’), los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

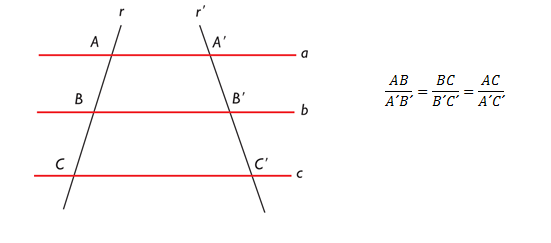
¿Para qué sirve aplicar el teorema de Tales? - Sirve a los alumnos para dividir un segmento en tres partes iguales, trabajando la proporcionalidad geométrica y aplicando el cálculo de longitudes de segmentos, (dos rectas que se encuentran en posición de Thales (2 rectas secantes, cortadas por varias rectas paralelas)). 

ACTIVIDADES PARA CASA: 

Ejercicio 1

Las rectas a y b del dibujo son paralelas. Comprueba utilizando el teorema de Thales si también lo es la recta c.

SOLUCIÓN EJERCICIO 1: ¿Cómo demostramos que la recta c es paralela?

Debemos saber demostrar que las rectas están en posición de Thales y que se cumple el teorema de Thales, comprobando si los segmentos de ambas rectas tienen la misma razón y sean proporcionales entre sí.

• Calculamos la razón de los primeros segmentos (a y b):

• Y la razón de los siguientes dos segmentos (b y c):

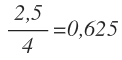
La razón es la misma, por lo que ambos pares de segmentos son proporcionales. Se cumple el teorema de Tales por lo que la recta c, es paralela.

Ejercicio 2

¿Cuánto mide el segmento (x) en este dibujo? 

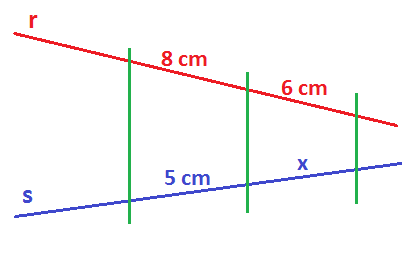
SOLUCIÓN EJERCICIO 2: Sabemos lo que miden los dos segmentos de (r), pero falta por saber cuánto mide uno de los segmentos de (s), por lo que a ese segmento le llamamos (x).

Según el teorema de Tales, los tramos enfrentados tienen la misma razón, por lo que sus divisiones deben dar mismo resultado por lo que las podemos igualar:

Nos queda una ecuación de primer grado, la cuál tenemos que despejar la X.

• Para resolver esta ecuación, pasamos los denominadores de cada miembro, multiplicando al numerador del miembro contrario (multiplicamos en cruz).

• Ya no tenemos denominadores. Vamos a despejar la X. Ahora, el 8 que está multiplicando a la x, pasa al segundo miembro dividiendo:

• Y finalmente operamos para calcular el valor de X:

Al comprobarlo, resulta que los pares de segmentos son proporcionales.