Trigonometría: Concepto de Ángulo, clasificación y ángulos en el plano cartesiano
En Junio como ultimo tema vamos a ver un tema sobre Trigonometría y tocaremos los puntos que vemos en el titulo.
CONCEPTO DE ÁNGULO
Porción indefinida de plano limitada por dos líneas que parten de un mismo punto o por dos planos que parten de una misma línea y cuya abertura puede medirse en grados.
Figura formada por dos elementos unidos por un extremo
CONSTRUCCIÓN DE ANGULOS
CLASIFICACIÓN DE ÁNGULOS
Ángulos según su tamaño
- Ángulo agudo: es aquel que mide menos de 90 grados, y más de 0°. Por ejemplo, en un cono de helado puedes distinguir este tipo de ángulo.
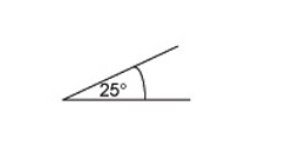
Ángulo agudo - Ángulo recto: este ángulo mide 90°, siendo sus lados perpendiculares entre sí. Un ejemplo sencillo, seria ver la letra L.
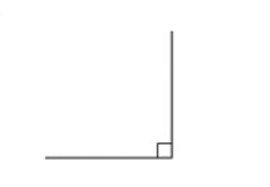
Ángulo recto - Ángulo obtuso: cuando el ángulo que se forma entre dos rectas supera los 90° pero es inferior a los 180° estamos hablando de uno obtuso. Un ejemplo sencillo es ver la apertura de un abanico.
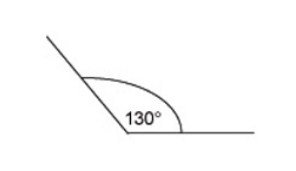
Ángulo obtuso - Ángulo llano: si sumamos dos ángulos rectos, nos da como resultado un ángulo llano, es decir, mide igual a 180°. Un ejemplo sencillo es un brazo estirado, el ángulo que se forma entre el brazo y antebrazo es uno llano.
Los ángulos también pueden clasificarse a gran escala como convexos (menor a 180 grados) o cóncavos (superior a 180°).
Ángulos según su posición
Se clasifican en consecutivos, adyacentes, y opuestos.
- Ángulos consecutivos: son dos ángulos que comparten su vértice y uno de sus lados.
- Ángulos adyacentes: siguiendo la idea anterior, dos ángulos son adyacentes cuando tienen el vértice y un lado en común y el otro lado es una prolongación del otro, formando un ángulo llano.
- Ángulos opuestos al vértice: los lados de uno son la prolongación del otro, teniendo un mismo vértice.
Ángulos según su suma
Según la suma de los ángulos estos pueden clasificarse en complementarios y suplementarios:
- Ángulos suplementarios: son aquellos que al sumarse dan un total de 180 grados.
- Ángulo complementarios: si ambos ángulos al sumarse dan como resultado 90°, entonces son complementarios.
ÁNGULOS EN EL PLANO CARTESIANO
Las características de un ángulo orientado en un sistema cartesiano son:
Ø Su vértice coincide con el origen de coordenadas.
Ø Está generado por la rotación de una semirrecta con origen en (0;0). La semirrecta parte desde una posición inicial coincidente con el semieje positivo de las x y gira manteniendo fijo su origen hasta llegar a una posición que marca su lado terminal.
Ø El ángulo es positivo cuando está generado en sentido contrario al movimiento de las agujas del reloj y negativo cuando está generado en sentido horario.
Ø La rotación de la semirrecta puede ser mayor que un giro.

En el gráfico se muestran tres ángulos que tienen el mismo lado terminal:
· positivo de 30 º (menor que un giro)
· negativo de 330º (menor que un giro)
· positivo de 390º (mayor que un giro)
Se considera al plano cartesiano dividido en cuatro sectores llamados cuadrantes:

Se determina en cuál de los cuadrantes se encuentra el lado terminal del ángulo y esta posición da la ubicación del ángulo. El lado terminal de los tres ángulos representados está en el primer cuadrante por lo que todos ellos pertenecen a dicho cuadrante
EJERCICIOS
1)a) Representa en un plano cartesiano los siguientes ángulos:
· 165°
· - 50°
· 840°
· 230°
b) Indica en qué cuadrante está cada ángulo.
2) Considera el ángulo 7/5 π rad.
a) Expresa su medida en sistema sexagesimal.
b) Represéntalo como ángulo orientado en un plano cartesiano
c) Indica la amplitud un ángulo negativo menor que un giro que tenga el mismo lado terminal que él.
3) Completa con la amplitud de un ángulo positivo mayor que un giro:
Los lados terminales de un ángulo orientado de 50° y un ángulo de …………. son coincidentes.







No hay comentarios:
Publicar un comentario